this post was submitted on 25 Aug 2024
575 points (98.5% liked)
Map Enthusiasts
3518 readers
19 users here now
For the map enthused!
Rules:
-
post relevant content: interesting, informative, and/or pretty maps
-
be nice
founded 2 years ago
MODERATORS
you are viewing a single comment's thread
view the rest of the comments
view the rest of the comments
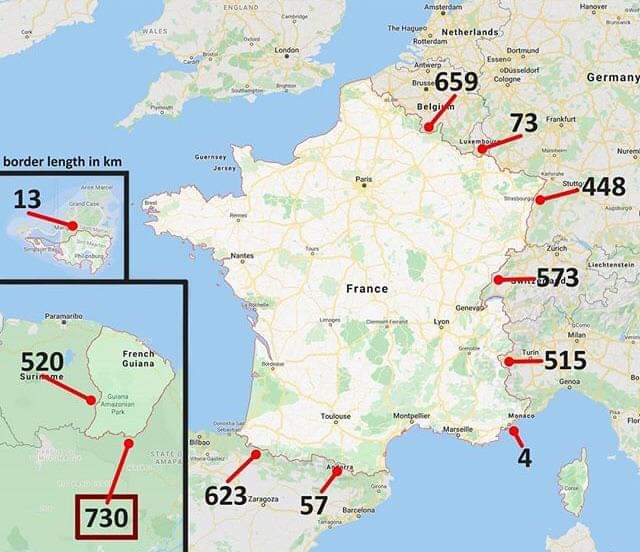
Arnt most borders fractals so can any border be the largest?
No, because borders are made up by humans and humans can't write down or even measure infinitely small
Some borders drawn as straight lines on maps sure. But we also define borders by rivers and all sorts of other fractal things.
Borders are just social construct
We can if we make tools to do it for us.
halting problem
Actually, in this case, it's easily solved. Trying to measure an infinitely complex curve will never halt, answer found.
No, I can write limits.
It's kind of subtle how exactly you're using numbers when writing limits. You're either not actually doing infinitesimals, just Cauchy sequences centered around a point, or you are and you get to enjoy the axiomatisation of the hyperreals.
You'll have to represent each border on the same scale, so no. Also, why are you being flagged as a bot?
I was writing a bot and must have accidentally enabled it for my main account. Fuck im retarted.
Even Firefox's coloured containerisation can't fix stupid
LIES!!! AI IS TRYING TO INFILTRATE US!!! BURN THE BOT WITCH!!!!
Your username is cursed, thanks for bringing that combination of words to life
Don't thank me, thank chatGPT.
Anyone can just go into their account settings and mark their accout as a bot. Idk why you would though
You would do that if you were running that account using a bot.
Yes, but non-coastal borders become nice curves at a certain resolution just because they're legally defined by points.
Coastal borders are legally vague AFAIK, since they're defined as a nautical mile from "the shore" or something like that, but when you're already on the ocean a matter of a few meters tends not to matter.
considers
Well, they aren't fractal, that's for sure.
It is true that we could make borders more-closely-map to physical features, and that would increase the length somewhat.
And we can define borders however we want, so that's up to us.
But ultimately, matter is quantum, not continuous, so if we're going to link the definition of a border to some function of physical reality, I don't think that we can make a border arbitrarily long.
Coastlines are indeed fractals, and a similar argument could be made for any border defined by natural phenomena (so like, not the long straight US/Canada border).
Coastlines are not self repeating and they are fundamentally finite.
I believe they were referring to this, where technically a coast could be seen as similar to fractals
https://en.wikipedia.org/wiki/Coastline_paradox
Literally from that page
Fractals are not necessarily self repeating, they just contain detail at arbitrarily small scales.
Which a physical space cannot fulfill
Fractals are not required to be self-repatiing. For example, the Mandelbrot set is a non-self repeating fractal pattern.
And please elaborate on how they are fundamentally finite.
Coastlines exist in the real world, they are by definition finite structures. You can only zoom in to them so far before the structure is no longer a coastline.
Thats making a lot of assumptions about quantum physics
An atom is not a coastline, even if it is a piece of one
Well, quantum mechanics is continuous, just in a way that often maps to discrete things when measured. I'm sure someone has written a research paper on quantum law, but I wonder if anyone who actually knows quantum mechanics has.
It is only continuous because it is random, so prior to making a measurement, you describe it in terms of a probability distribution called the state vector. The bits 0 and 1 are discrete, but if I said it was random and asked you to describe it, you would assign it a probability between 0 and 1, and thus it suddenly becomes continuous. (Although, in quantum mechanics, probability amplitudes are complex-valued.) The continuous nature of it is really something epistemic and not ontological. We only observe qubits as either 0 or 1, with discrete values, never anything in between the two.
Sure, but if you measure if a particle is spin up or spin down in a fixed measurement basis, physically rotate the particle, and then measure again the amplitudes change continuously. You could also measure it in another basis, which themselves form a continuous family, and get a similarly logical answer (although not independently of the first one). I don't know much about quantum field theory, but I do know that fields in it are continuous, just like they are in classical theories.
All in all, while quantum logic is part of what makes it continuous, I think I'd still stand by that it is continuous.
Longest*
How did you get that wrong when it's correct in the title...?
And what you're talking about is not borders, it's coasts. Borders are much more specific since they're completely made up by us. They have very specific lengths.
It's actually impressive how much you got wrong in your comment. If I was in the same class as you, I would have worked hard to never be in the same group as you because it's pretty certain you've failed to understand many other simple and obvious things. I'm almost curious about what other things you've misunderstood.
Yeah, you're honestly way out of line here.
Being correct is not a virtue. Other people are not impressed by how correct you are, or by how great a job you've done in correcting others.
Knowing more than others is not a virtue. Literally everyone knows less about some things than others; there is no super genius that is right or most knowledgeable about everything. For that reason (and many others), lack of knowledge is not a good reason to treat someone poorly.
You obviously care about the mechanics of clear communication. I believe that you can be better than this, that you can keep in mind why we communicate, not just how. You obviously know a lot about certain topics as well. I believe you can be better at how you demonstrate your knowledge. This time you showed off your knowledge to shame someone else. Maybe next time you could show off what you know by sharing it with someone in a helpful way.
Then people really would be impressed.
Wow, you're an asshole. Many borders are (or were) defined by positions of natural features though, so no you're wrong. They aren't completely made up by us. They are made up, but based on nature.
Wow, what the fuck happened to you to make you like this? It's a post about a map.
It's called a synonym. Get yourself a Thesaurus and read it.
I too would avoid being the team with you, considering your commitment to being an asshole.