this post was submitted on 14 Aug 2024
909 points (96.6% liked)
Facepalm
371 readers
1 users here now
Anything that makes you apply your hand to your face.
founded 4 months ago
MODERATORS
you are viewing a single comment's thread
view the rest of the comments
view the rest of the comments
Fractions are easier to do calculations in your head or on paper than trying to do the same stuff in decimals. E.g. half of 1/2 is 1/4, half of 1/4 is 1/8, half of 1/8 is 1/16, half of 1/16 is 1/32 etc. In decimals this would be 0.5 -> 0.25 -> 0.125 -> 0.0625 -> 0.03125. When building stuff, I find it useful to be able to do that kind of stuff in my head easily.
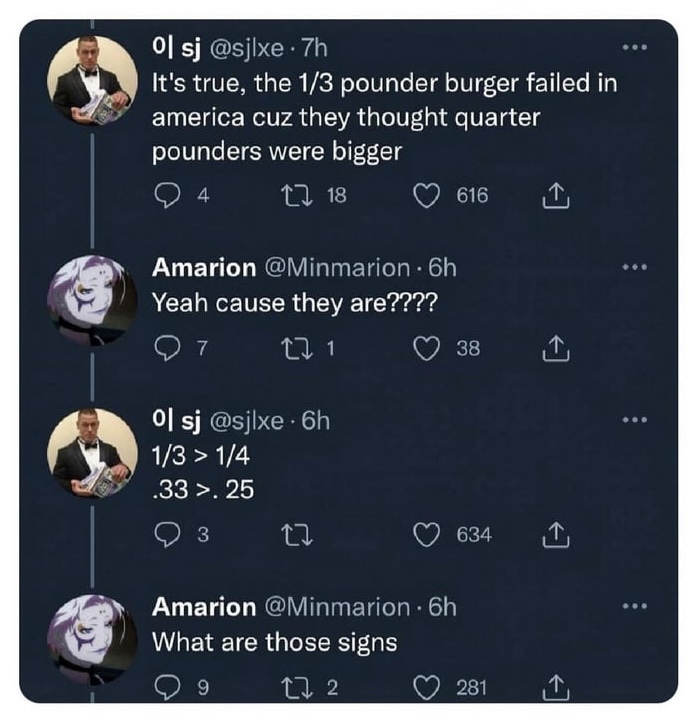
Tell me you're American without telling me you're American.
:) I think British woodworkers also use fractional units.
The problem occurs when you have a 1/4 pound burger for $1 and a 1/3 pound burger for $1.25. Is it worth it?
If only using fractions in powers of 2 1/2, I understand that it's simpler. A carpenter is happy to meassure 3/16s of an inch, since the tools have notches or marks for that. But when you include other fractions, it becomes messy.
How much more is 1/3 than 1/4? Instead of handling digits, you have to find the lowest common denominator to perform the subtraction. I.e. 1/3 - 1/4 = 4/12 - 3/12 = 1/12.
And at this point, I believe the relationship to the units are lost. Do you have any direct sense to what 1/12 of a pound is?
The 1/3 pound burger is (1/3)/(1/4) times the size of the 1/4 pound burger. So the burger is worth it if $1*(1/3)/(1/4) is greater than $1.25. We arrive at $4/3 which we want to compare to $1.25. Now, since we are relating units which use fractions to units where fractions are unusual, we have another problem. (Yes, we can easily see tha 4/3 = 1.333..., but we wanted to use fractions, right?). So to compare the numbers, we can see that 1.25 = 125/100, which we can simplify to 5/4. So in the end we are left with the simple problem of finding which is bigger between 4/3 or 5/4.
To summarize, I agree that fractions are nice when you have them in a vacuum and don't have to relate them to numbers of other units.
why use decimals when you can use the... you know, actual weight of the thing?
How is saying “this weighs .25 kg“ not using the “actual weight of the thing”?
I get what you mean, but its adding a useless complexity layer.
If the thing always is smaller than, for example, a kilogram, just use the next measurement unit, a gram. 100g, 200g, 500g, etc.
It's true the other way around, if the thing is always bigger than, for example, a kilogram, use it as is. 1kg, 1.5kg, 4kg, 6.2kg.
For ease of comparison, always use the most significant unit.