@Onionguy@lemm.ee wir werden gerufen
eunieisthebus
Vortrefflich erkannt.
Neben der fehlerhaften Typografie finden sich auch noch inhaltliche Ungereimtheiten. Bspw. haben wir n+1 Elemente a_0 bis a_n im Tupel der aus der Menge n elementigen Tupel stammen soll.
Mobil ist das die lazy Lösung ^^"
Oder wie bei den öffentlich rechtlichen und der Verweildauer der Mediathek Inhalte.
... Oder wie bald die öffentlich rechtlichen mit ihren Webinhalten.
Außerdem die Formel besser direkt absetzen
\[ ... \]
Stilistischer Punktabzug weil du das schwarzer Filzstift im mathmode hast anstatt ein \text{ } drumzupacken.
Dir ist aber schon klar dass du das Standardprogramm für eine Dateikennung manuell festlegen kannst?
Auch wenn ich den anderen hier zustimmen möchte, es lieber sein zu lassen, verlinke ich hier den Klassiker: https://www.youtube.com/watch?v=4o5hSxvN_-s
Jein. Das ist so ne Sache. Also wie GIMPS im Detail funktioniert, ist auf ihrer Seite erklärt. Hier etwas allgemeiner. Wenn du nach einer großen Primzahl suchst gehst du so vor:
-
Wähle eine beliebige / die zu testende Zahl.
-
Teste einfache Faktorisierungsalgorithmen ob sich ein kleiner Faktor findet. Probedivision ist ineffizient. Da gibt es bessere Algorithmen wie die verschiedene Sieb Algorithmen (quadratisches oder Zahlkörper Sieb etc.)
Wird dir irgendwann langweilig weil du nichts findest, machst du weiter mit.
- Führe einen PRP test durch (probable prime test) z.B. Miller-Rabin. Diese wiederholt man solange bis man entweder ein 'nicht prim' erhält oder die Wahrscheinlichkeit dass die Zahl prim ist dir hoch genug ist. Für das Beispiel miller rabin ist die Wahrscheinlichkeit dass eine nicht primzahl als 'wahrscheinlich prim' erkannt wird pro run kleiner 50% (zwei runs also 25% usw.)
In den meisten Anwendungen ist das genug und man ist zufrieden. (Im übrigen auch für den gesamten Kryptographie Kram. Also womöglich hackt sich jemand irgendwo bei dir rein weil dein private rsa key doch nicht nur zwei Primfaktoren hat ;). Wenn es genau sein muss wie auch hier in Gimps kommt:
- Ein Exakter Primtest. Probedivision bis zur Quadratwurzel hat exponentielle Laufzeit. Auf dem papier geht das aber praktisch unbrauchbar. Normalerweise suchst du nach einem primtest der speziell für deine Anwendung funktioniert. Im Fall von mersenne Zahlen ist das lukas-lehmer. Der Algorithmus ist auf der Seite erklärt.
Fun fact: während man zwar nicht weiß ob Faktorisierung polynomiell geht, liegt prim testen sicher in P. Es gibt den AKS primzahltest. Nur ist der ein Paradebeispiel warum Komplexitätsklassen praktisch nicht unbedingt sinnvoll sind. Die Konstanten sind so groß, dass er trotzdem 'ewig' brauch.
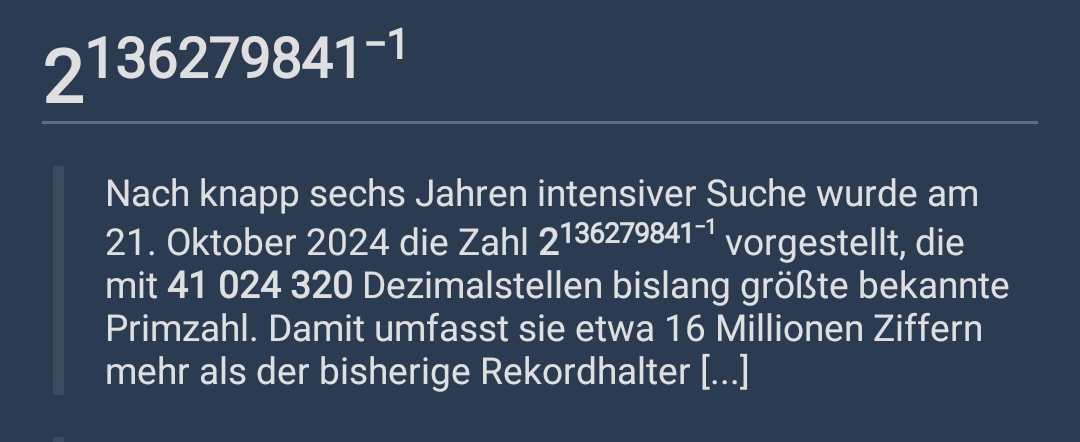
Wenn für dich alles richtig ausschaut, kanns auch an meinem Client liegen. Mir fehlt eine Leertaste vor der -1 damit die nicht im Exponent steht.
The left one ist for your left vagina and the right one for your right vagina. Duuuuuh. Stupid question.
Dann will ich stattdessen ein
\DeclareMathOperator in der Präambel 🤓