- Show that the infinite multiplication
(1+1/1)(1+1/2)(1+1/3)...does not converge.
this post was submitted on 16 May 2024
3 points (100.0% liked)
Daily Maths Challenges
189 readers
1 users here now
Share your cool maths problems.
Complete a challenge:
- Post your solution in comments, if it is exactly the same as OP's solution, let us know.
- Have fun.
Post a challenge:
- Doesn't have to be original, as long as it is not a duplicate.
- Challenges not riddles, if the post is longer than 3 paragraphs, reconsider yourself.
- Optionally include solution in comments, let it be clear this is not a homework help forums.
- Tag [unsolved] if you don't have a solution yet.
- Please include images, if your question includes complex symbols, attach a render of the maths.
Feel free to contribute to a series by DMing the OP, or start your own challenge series.
founded 6 months ago
MODERATORS
you are viewing a single comment's thread
view the rest of the comments
view the rest of the comments
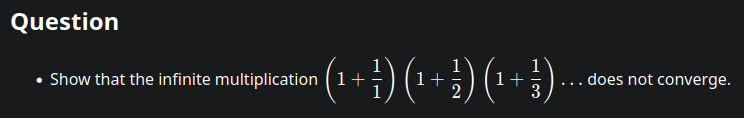
::: spoiler solution Isn't this already the result of your 1st formula? As the denominator of the last fraction you wrote down,
(n+1)/n, cancels out with the counter of the one right before,n/(n-1), which you didn't write down. Thus the whole product up to the nth term reads after cancellation of neighbouring counters and denominator pairs(n+1)/1 →∞ when n→∞.